How to Calculate Weight Watchers Smart Points

This is the equation that we use to calculate the SmartPoint™ value of your food or drink items (long-hand on top, short-hand on bottom). I will be using the short-hand variation in the following excerpt.
So, that’s great and all but how is it even possible to know this is the exact equation, and then be able to solve for 4 unknown variables (those seemingly random multipliers for each food nutrient)? At least this is what I was thinking when I first started investigating the science and math behind these smart point calculations. It was nice to benefit from someone else’s work, but it bothered me I wasn’t certain it was accurate, so I decided to reverse engineer it.
This is how I did it.
If you’re starting from scratch, there’s not much information to work with. But you do know that:
- Calories, saturated fat, sugar, and protein are somehow combined to represent a food or drink item in the form of a number.
- Saturated fat and sugar increase this number, but protein decreases it.
- All foods and drinks can be represented in the form of this integer, which is generally less than 10 points per food or drink item.
- This integer is rounded to the nearest whole number.
So, given this set of data, how can we convert it into the equation we see above?
Well, we can start with what we know. The first two data points tell us that the SmartPoint (SP) value is calculated using calories (C), saturated fat (F), sugar (S), and protein (P). Saturated fat and sugar add to this number while protein subtracts from this number. We can infer from this information the following:
Next, we can use our third data point to further develop our equation. We know that the SmartPoint integer is some magnitude less than the raw addition and subtraction of the nutrients in a food. To factor this in, we need to choose one of the two following methods:

OR

Both are completely valid, but I’m going to stick with the top one since that’s the one we use and the one I solved. Finally, we need to account for the variance of rounding, but to simplify things I will wait and demonstrate how that’s done later on.
Ok great, we’ve derived an equation for the SmartPoint, but we have a new puzzle in front of us, how are we going to solve for 4 unknown variables? I suppose it’s theoretically possible to guess and check? Although that might take a while, even if you’ve developed efficient programmatic functions to do the heavy lifting.
The route I took was to cut down on the number of unknown variables we need to solve because 4 is too many. The easiest way to do this is to find a food or drink that contains sugar, but no fat or protein. This will reduce the unknown variables to 2 because fat and protein will be 0 regardless of their multipliers.
The food or drink type that came to me first was sugary drinks! Not only would the right one fit the criteria above, but we need something with total calories that come from sugar alone. For example, if we chose 12oz of orange juice, its total calories stem from proteins and other nutrients. Thus, as our ounces of orange juice increase, so too would the skew of our data.
Due to this, I chose a can of regular Coca Cola. One can of coke contains 240 calories, 75mg of sodium, and 65g of sugar. Since sodium does not contain calories per se, this fits all of the criteria we are looking for. Now we can ask our myWW app what the SmartPoint value of a can of coke is, and temporarily simplify our equation.
FROM:

TO:
Although WW tells us the SmartPoint value is 15, we know that number is rounded. So let’s account for that in our simplified equation:
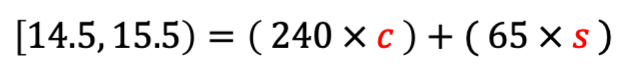
This means that the SmartPoint value is at least 14.5, but less than 15.5. Mathematically, it would look like this:
I don’t think it’s necessary to go through each line of the code I wrote to represent this, however, I’ll briefly explain what it does (if you’re interested in it though, you can find it on my GitHub). Essentially, what we need to do is find all possible solutions for c and s, then take the average of those values.
For example, if I wanted to run through all solutions to the hundredth percentile, the values for c and s would look something like this:
| c | 0.01 | s | 0.01 |
| c | 0.01 | s | 0.02 |
| c | 0.01 | s | 0.03 |
| c | 0.01 | s | 0.99 (all the way to .99) |
| c | 0.02 | s | 0.01 |
| c | 0.02 | s | 0.02 |
| c | 0.02 | s | 0.03 |
| c | 0.02 | s | 0.99 (all the way to .99) |
And so on (although in my calculations I went a bit deeper, incrementing to the thousandth percentile). The goal is to iterate through each possibility, incrementing each value by a hundredth, until all possible solutions for c and s are calculated for a smart point value greater than or equal to 14.5 but less than 15.5.
The results for this example calculation are:
| c | 0.01 | s | 0.19 |
| c | 0.01 | s | 0.20 |
| c | 0.02 | s | 0.15 |
| c | 0.02 | s | 0.16 |
| c | 0.03 | s | 0.12 |
| c | 0.04 | s | 0.08 |
| c | 0.04 | s | 0.09 |
| c | 0.05 | s | 0.04 |
| c | 0.05 | s | 0.05 |
| c | 0.06 | s | 0.01 |
Then, the arithmetic mean of those results: c = 0.032 and s = 0.11
Close, but the original equation states c = .0305 and s = .12, so where did we go wrong? Should we go back to the drawing board?
Well, not quite yet. As I’ve mentioned before, because smart points are rounded, we are going to be dealing with averages, which means we need a sufficient sample size to cut through the variance and develop a multiplier closer to a foods actual SP number. For instance, conducting these calculations on the arithmetic mean of 10,000 cans will bring us much closer to the true SmartPoint value. This way we don’t gyp anyone out of their points!
Because I wanted to do this without referencing any external equations, I had to scan a few more cans of coke to see how each one influenced the overall smart point value. I ended up scanning 75 cans in the app, so they’re probably worried about me, but it got the job done. What I was looking for was a repeatable pattern in the results, and I found one. The pattern looked like this:
| 8 | 8 | 9 | 8 | 8 | 9 | 8 | 8 | 9 |
What this means is that the 8th can of coke costs 16 smarts points, the next 8th can costs 16 points, but the following 9th can costs 16 points, then it repeats. I applied this pattern to represent what 100, 200, and eventually 10,000 cans of coke would cost in SmartPoints, ran it through the functions I built, and took the mean of those results. This is what that calculation produced:
| c | = 0.030500000000000003 | s | = 0.11999999999999998 |
And if we simplified it:
| c | = 0.0305 | s | = 0.12 |
Boom, the exact values in the accepted equation for calories and sugar. Now that we have successfully solved for 2 of the 4 unknown variables in the original equation, we can add those to the one we built:

That was the tough part or at least the programmatically intensive part. From here on, we can apply the same concepts we used to solve for c and s to acquire f and p, our multipliers for saturated fat and protein.
So, I picked a food that contains protein, but no saturated fat - the Idaho Potato - then manipulated our current equation using simple algebra to solve for little p.
Idaho Potato
| Calories | 110 |
| Saturated Fat | 0 |
| Sugar | 1 |
| Protein | 3 |
| SmartPoints | 3 |
Pretty far off from our .098 multiplier in the original equation. But let’s not forget about deducing a number closer to the true SmartPoint value through increasing the sample size. So I expanded the calculation to 10,000 Idaho potatoes and once again took the average of those results:
| p | = 0.0980064999999842 |
And if we simplified it:
| p | = 0.098 |
Again, the exact value that's used in the original equation. Now that we’ve successfully solved for the protein multiplier, let's add it to ours:

Ok, the final piece to this puzzle is to solve for f, our saturated fat multiplier. No need to reiterate the process, I chose a Hot Pocket for this because it was the first food I thought of.
Hot Pocket
| Calories | 600 |
| Saturated Fat | 12 |
| Sugar | 5 |
| Protein | 19 |
| SmartPoints | 20 |
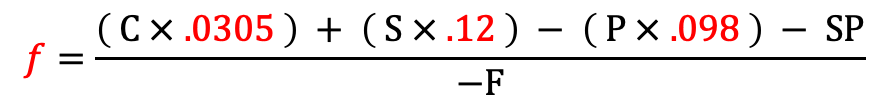
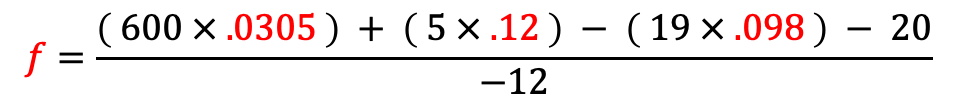
Close, but no cigar. For the last time, we’ll increase our sample size, take the arithmetic mean of 10,000 hot pockets, and the result is:
| f | = 0.2750094974423127 |
And if we simplified it:
| f | = 0.275 |
Alas, we have officially reverse-engineered the SmartPoint value equation and can confirm with certainty that it’s accurate. To wrap things up, let’s add the final value for our saturated fat multiplier and complete the equation.